Draw The Floor Plan Of A Galley With Three Vertices

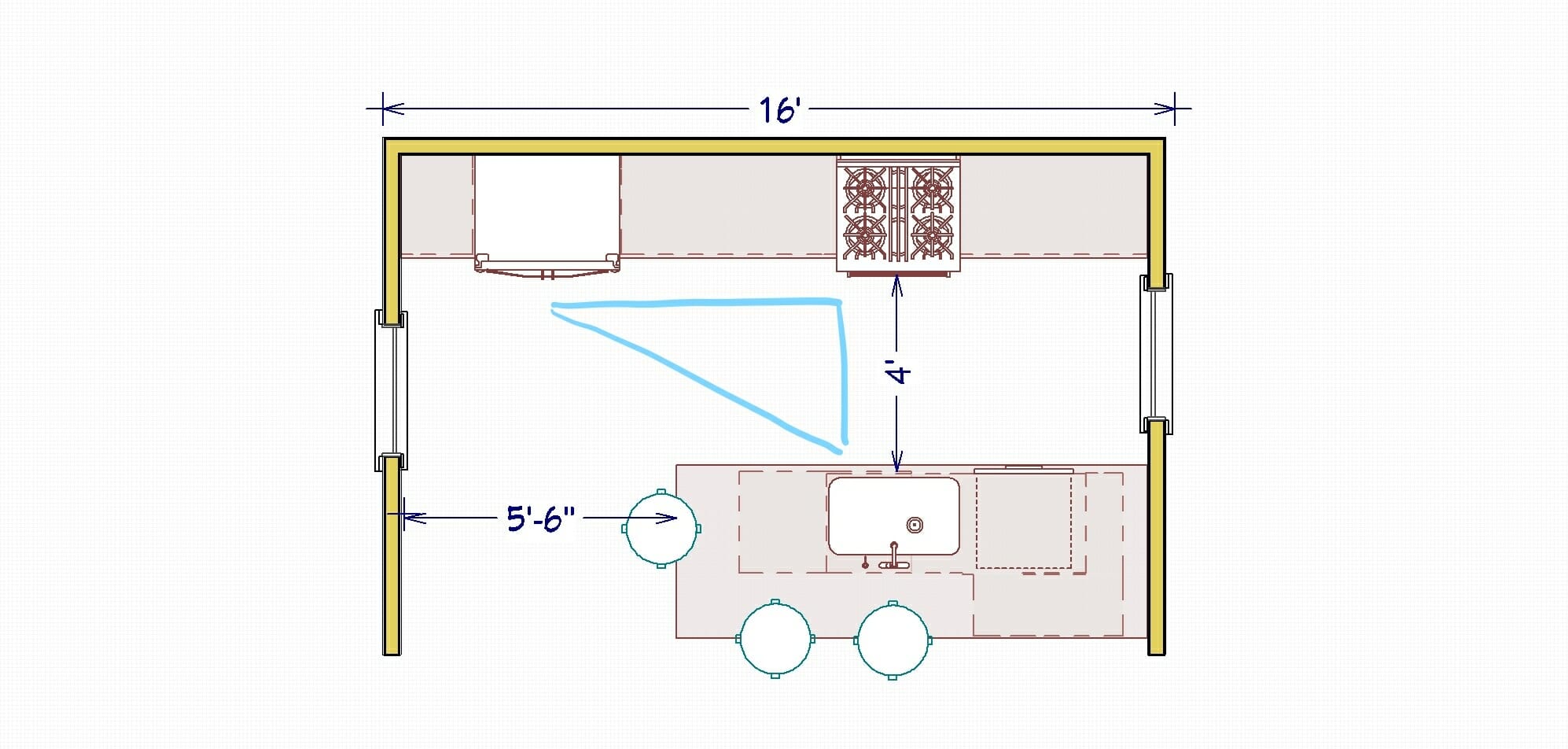
Draw the floor plan of an art gallery with straight walls that has 16 vertices and needs 3 6 marks guards.

Draw the floor plan of a galley with three vertices.

Show transcribed image text. Now consider any triangulated polygon with n 3 n 3 n 3 vertices. If v 3 is not an integer then the number of vertices needed is the biggest integer less than v 3. Floor plans typically illustrate the location of walls windows doors and stairs as well as fixed installations such as bathroom fixtures kitchen cabinetry and appliances.

When your floor plan is complete create high resolution 2d and 3d floor plans that you can print and download to scale in jpg png and pdf. Pick any two vertices u u u and v v v that are connected by a diagonal i e connected by an edge in the triangulation but not in the original polygon. Draw the floor plan of a gallery with three vertices. Draw floor plans of three art galleries of this type that require 1 guard 2 guards and 3 guards respectively.

Draw a floor plan add furniture and fixtures and then print and download to scale it s that easy. This problem has been solved. Circle the positions of the guards. Then there are v 3 vertices from which it is possible to view every point on the interior of the curve.

Carefully explain why 3 guards are needed. What is the smallest number of guards you need. For n 3 n 3 n 3 the polygon is a triangle and we can choose three different colors for the three vertices. What shape do you get.